 |
Algorithm |
 |
Effective Mine Hit Rate |
 |
Hitting Two Minefields |
 |
Why? |
 |
Credits |
 |
Articles |
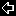 |
VGAP Main Page |
Tim's movement algorithms contain a number of artifacts which make mine hits a little more complicated than rolling a dice. This analysis has been published first in May 2003, in news:alt.games.vga-planets, articles <1053339626.irz765%sr21@inf.tu-dresden.de> and <1053427025.irz750%sr21@inf.tu-dresden.de>. It has been merged and reformatted for this web page in October 2009.
The analysis started when people noticed that web mine hit odds aren't exactly 5% as configured. Andreas Huck from Tholian Strategic Headquarters (now defunct?) finally backed those observations by running thousands of sims and doing a little statistics. So I sat down with a decompiler, to find out what really happens. The code fragments on this page are pseudo-code produced by that decompiler.
Warning: hefty technical details follow.
Algorithm
Let's start with the dirty details: Mine hits are processed within a routine I call Mine_hits. It takes six parameters:
- X, Y: position of the ship
- LY_through_mines: counts how many mines we've passed, for generating the messages
- Stop_flag: set to one after a Web hit. Movement will stop when this flag is set
- Scale: an obscure parameter with interesting effects, we'll see more on that later.
- Num_mines: Before moving each ship, HOST prepares an array "Minefield_array" with all minefields which can possibly affect the ship. Num_mines is the number of mines in that array.
SUB Mine_hits (X, Y, LY_through_mines, Stop_flag, Scale, Num_mines)
/* some initialisation */
FOR i:=1 TO Num_mines DO
Mine_id := Minefield_array[i]
IF /* ship is inside mine field */
LY_through_mines += 1
IF /* normal mine field */
/* [snip] */
ELSE
As you see I have omitted quite a lot red tape. Nothing spectacular here, just some pythagoras tests, allies etc.
IF (Config_web_hit_rate * Scale >= Trunc(rand * 100)) AND (Ship_owner<>7) THEN
Three surprises in one line. (Well, almost.):
- The web hit odds are scaled by an obscure factor. We'll remember that for later.
- Assuming that the factor is 1, web hit odds still are too high. If you configure 5%, the ">=" test will still yield true in 6 out of 100 cases. The relation sign should be ">", or the Trunc should be dropped.
- Crystals never hit web mines. A well-known misfeature.
To summarize, the web hit rate is Trunc(scale * config) + 1.
The following code says what the ship does after hitting a mine:
load_hull (Ship_hull)
Ship_DX := 0
Ship_DY := 0
Ship_Speed := 0
Clear waypoint and speed.
Fuel_loss := Trunc(Ship_Fuel / 6)
IF Fuel_loss < 50 THEN Fuel_loss := 50
Ship_Fuel -= Fuel_loss
IF Ship_Fuel < 0 THEN Ship_Fuel := 0
Drain fuel. You know it. No surprise here.
Stop_flag := 1
Tell movement that this ship should stop. Note that this does not stop the "for-all-minefields" loop, so you can hit another web this turn. Even another normal mine. That's what Andreas observed.
IF Hull_mass>0 THEN
Damage_taken := ERnd(1000 / Hull_mass)
Ship_damage += Damage_taken
/* Send message */
ENDIF
Nothing surprising here.
Save_ship
ENDIF
ENDIF
/* ... */
ENDIF
NEXT
ENDSUB
Okay, now where does that obscure factor come from? Let's take a peep at the movement main code:
Delta_X := /* X displacement */ Delty_Y := /* Y displacement */ Abs_DX := Abs(Delta_X) Abs_DY := Abs(Delta_Y) ... IF Abs_DY < Abs_DX THEN Scale := sqrt((Delta_Y1 ^ 2) / (Delta_X1 ^ 2) + 1) ELSE Scale := sqrt((Delta_X1 ^ 2) / (Delta_Y1 ^ 2) + 1) ENDIF
Movement uses the Bresenham algorithm. When moving 1 ly along the major axis, it uses a smaller step along the minor axis. For example, when you're going 10 ly right and 2 ly up, the ship will make 10 steps, each one 1 ly to the right and 0.2 ly up. The length of each of these steps, slightly more than 1 ly, is computed above as Scale. See Movement on Donovan's VGAP Help Pages for details on movement.
Effective Mine Hit Rate
We have seen that movement happens in steps of different size, and that those use different mine hit odds. To be able to compare them, we'll now compute an effective hit rate.
The number of steps used for a particular distance Dist is
Steps = Dist / Scale
As seen above, the web hit rate per step is
Rate_Step% = Trunc(Config_web_hit_rate * Scale) + 1 Rate_Step = Rate_Step% / 100
The chance of not hitting a web mine in Steps steps is
(1-Rate_Step)^Steps
We want the effective rate Eff_Rate so that moving a distance of "Dist" yields the same probability:
(1-Rate_Step)^Steps = (1-Eff_Rate)^Dist (1-Eff_Rate) = (1-Rate_Step)^(Steps/Dist)
From the first formula, we have that Steps/Dist is precisely 1/Scale. Also, add and subtract around a bit to receive the final formula:
Eff_Rate = 1 - (1-Rate_Step)^(1/Scale)
Now let's compute Scale. For simplicity, we assume to move somehow between 0 and 45 degrees. All other angles are symmetric to that.
Delta_X1 = Dist*sin(angle) Delta_Y1 = Dist*cos(angle)
This yields the second case in the above IF, so
Scale = sqrt((Delta_X1 ^ 2) / (Delta_Y1 ^ 2) + 1)
Using tan=sin/cos,
Scale = sqrt(tan(angle)^2 + 1)
Using tan^2 = (1-cos^2)/cos^2 = 1/cos^2 - 1, this yields
Scale = 1/cos(angle)
Putting it all together, we end up at the following formula for the effective mine hit rate when moving through a minefield:
Eff_Rate = 1 - (1-(Trunc(Config_web_hit_rate / cos(angle))+1)/100)^cos(angle) Eff_Rate% = 100*Eff_Rate
This formula is hard to imagine, so here's a plot:
These are the rates you would use to compute your mine hit odds. For example, to compute the chance to successfully pass through 17 ly of webs at a particular angle, you would compute (1 - Eff_Rate)^17.
Note the two minima at about 33° and 44°. This means you minimize your risk of hitting a mine by moving along one of these angles.
Hitting Two Minefields
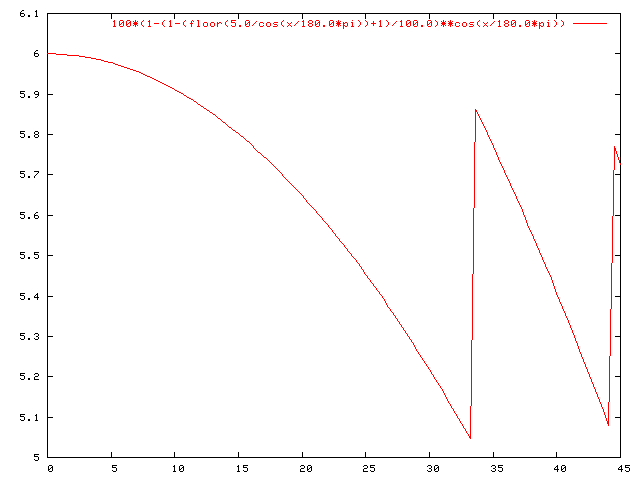
We have also seen that a mine hit only stops further movement, but doesn't prevent further mine hits. Assuming you are within two fields, and have already hit the first, the chance to hit the other one as well is precisely Rate_Step% from above. Graphically, it looks like this:
Summarized, from 0 to approximate 32 degrees, the chance to hit two minefields is 6%. From 32° to 43°, it's 7%, above that, it's 8%.
The average is 6.28%. That is, over all you web mine hits in all your games, 6.28% of all times you'll hit two fields with one ship.
Why?
Why is this so complicated? Where is the problem? Why can't the web hit rate not just be 5%, as documented?
If ships were moving one light-year at a time, we could indeed just roll a 5% die each step. But ships do not move in steps of one light-year. So we need to apply some mathematics. The problem is that Tim used an optimisation here which is not mathematically applicable. The correct formula for Rate_Step% would have been
Rate_Step% = 100*(1 - (1-Config_web_hit_rate/100)^Scale)
The used formula, Rate_Step% = Config_web_hit_rate*Scale, is a valid approximation for small values of Scale, but not for larger ones.
In addition, the actual comparison for mine hits, as noted above, contains a minor mistake, which amplifies the formula problem.
Credits
Andreas Huck gave the motivation to this analysis by publishing his experimental results. Those results agree with my mathematical derivations. Unfortunately, they are no longer online.